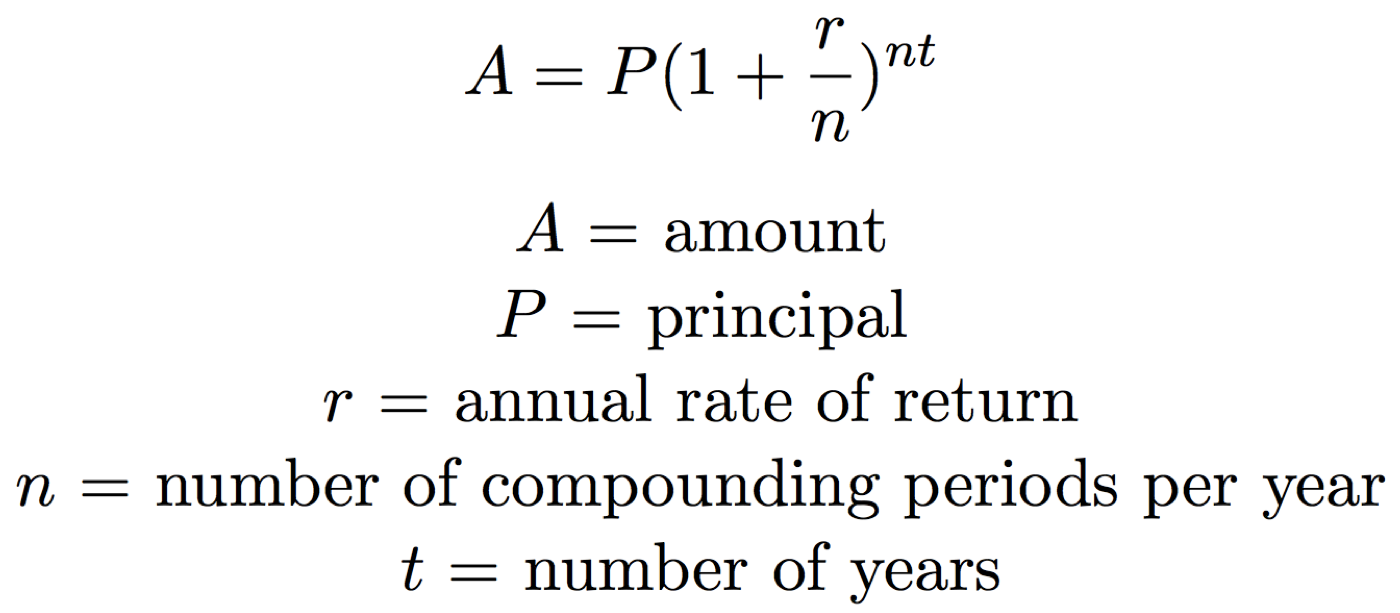
The calculations results given by the compound interest calculator serve only as guide for potential future value. Please speak to an independent financial advisor for professional guidance. FV – The FV function calculates the future value of an annuity investment based on constant-amount periodic payments and a constant interest rate. The final value after 5 years is $11,041 whereas with simple interest it would have been just $11,000. This might not seem like much, but if the rate of return is higher or the period over which compounding occurs is longer, the compounding effect can be dramatic. As shown by the examples, the shorter the compounding frequency, the higher the interest earned.

The Compound Interest Formula
If you have selected monthly contributions in the calculator, the calculator utilizes monthly compounding, even if the monthly contribution is set to zero. If the contribution frequency is annual, annual compounding is utilized, again if the annual contribution is set to zero. I hope you found this article helpful and that it has shown you how powerful compounding can be—and why Warren about wheres my refund Buffett swears by it. Again, we calculate twelve different future values, and we sum those future values to get the value in the account at the end of three years. That amount is compounded quarterly for the number of quarters remaining before the end of the three-year period. Think of this as twelve different compound interest calculations, one for each quarter that you deposit $135.
- The process repeats until at the end of three years, you deposit your last $135 that will not accrue interest since you are depositing it on the same day you are checking the balance in your account.
- The investing information provided on this page is for educational purposes only.
- You can use it to calculatehow long it might take you to reach your savings target, based upon an initial balance and interest rate.
- With monthly, you’ll earn (or be charged) interest each month, and with annual, you’ll earn (or be charged) every year (an annual percentage).
- That’s why it’s worth testing our compound interest calculator, which solves the same equations in an instant, saving you time and effort.
Investment details
Let’s go back to the savings account example above and use the daily compound interest calculator to see the impact of regular contributions. Compound interest is calculated by multiplying the initial principal amount by one plus the annual interest rate raised to the number of compound periods minus one. At year five the gap in return is more than $2,500 while at year ten it is over $15,000 on that same $10,000 initial investment. For a deeper exploration of the topic, consider reading our article on how compounding works with investments.
Compound Interest Formula With Examples
If you invested $10,000 which compounded annually at 7%, it would be worth over $76,122.55 after 30 years, accruing over $66,122.55 in compounded interest. More so if you look at the graph below, the benefits of compound interest outweigh standard interest by $45,122.55. Our online calculators, converters, randomizers, and content are provided “as is”, free of charge, and without any warranty or guarantee. Each tool is carefully developed and rigorously tested, and our content is well-sourced, but despite our best effort it is possible they contain errors. We are not to be held responsible for any resulting damages from proper or improper use of the service. Interest is the cost of using borrowed money, or more specifically, the amount a lender receives for advancing money to a borrower.
Inflation Rate
Following is the formula for calculating compound interest when time period is specified in years and interest rate in % per annum. Total Deposits – The total number of deposits made into the investment over the number of years to grow. As an example, $1000 with a fixed rate of return of 7% will take around 10 (72 divided by 9) years to become $2000. For instance, we wanted to find the maximum amount of interest that we could earn on a $1,000 savings account in two years. While compound interest grows wealth effectively, it can also work against debtholders. This is why one can also describe compound interest as a double-edged sword.
In order to make smart financial decisions, you need to be able to foresee the final result. The most common real-life application of the compound interest formula is a regular savings calculation. Many banks do offer compound interest accounts for savings accounts, certificates of deposit (CDs), and money market accounts. Each bank may vary in the compounding frequency, be it daily, monthly, or annually. The frequency that interest is compounded can have a large effect on the growth over time.
The following chart demonstrates the difference that the number of compounding periods can make for a $10,000 investment with an annual 7% interest rate over a 10-year period. Here’s how different compounding period intervals are affecting the total amount generated and interest earned. This is because rate at which compound interest grows depends on the compounding frequency, such that the higher the compounding frequency, the greater the compound interest. This formula takes into consideration the initial balance P, the annual interest rate r, the compounding frequency m, and the number of years t. Inspired by his own need to calculate long-term investment returns and simplify the process for others, Tibor created this tool.
If you turn on the “Inflation (%)” option, then you can also see the adjusted for inflation value as well. You can how over the chart bars to see individual metrics for any of the calculated yearly time series. Ancient texts provide evidence that two of the earliest civilizations in human history, the Babylonians and Sumerians, first used compound interest about 4400 years ago. However, their application of compound interest differed significantly from the methods used widely today. In their application, 20% of the principal amount was accumulated until the interest equaled the principal, and they would then add it to the principal.
Leave a Reply